Earth mover’s distance^•

Last modified on 01 Oct 2021.

What (general)?

• In statistics, the earth mover’s distance (EMD) is a measure of the distance between two probability distributions over a region D.^[ref]

• In stats or computer science, it’s “Earth mover’s distance”.
• In maths, it’s “Wasserstein metric”
• The Wasserstein distance is the minimum cost of transporting mass in converting the data distribution q to the data distribution p.

What (math way)?

The idea borrowed from this. The first Wasserstein distance between the distributions $u$ and $v$ is:

$l_1 (u, v) = \inf_{\pi \in \Gamma (u, v)} \int_{\mathbb{R} \times \mathbb{R}} |x-y| \mathrm{d} \pi (x, y)$

where $\Gamma(u,v)$ is the set of (probability) distributions on $\mathbb{R}\times \mathbb{R}$ whose marginals are and on the first and second factors respectively.

If $U$ and $V$ are the respective CDFs of $u$ and $v$, this distance also equals to:

$l_1(u, v) = \int_{-\infty}^{+\infty} |U-V|$

Example of metric

Suppose we wanna move the blocks on the left to dotted-blocks on the right, we wanna find the “energy” (or metric) to do that.

Energy = $\Sigma$ weight of block x distance to move that block.

Suppose that weight of each block is 1. All below figures are copied from this.

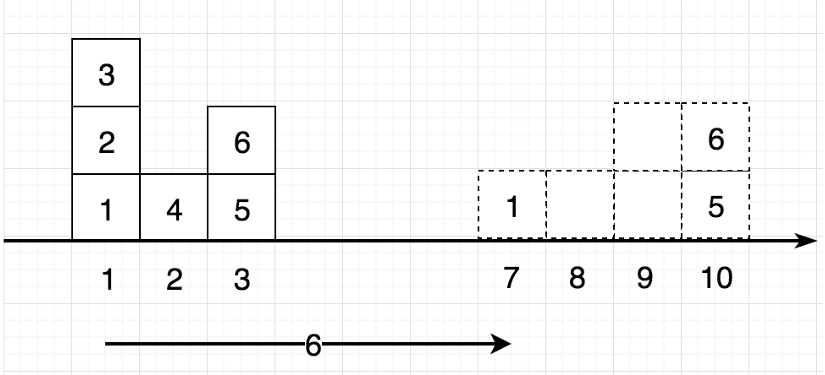
There are 2 ways to do that,

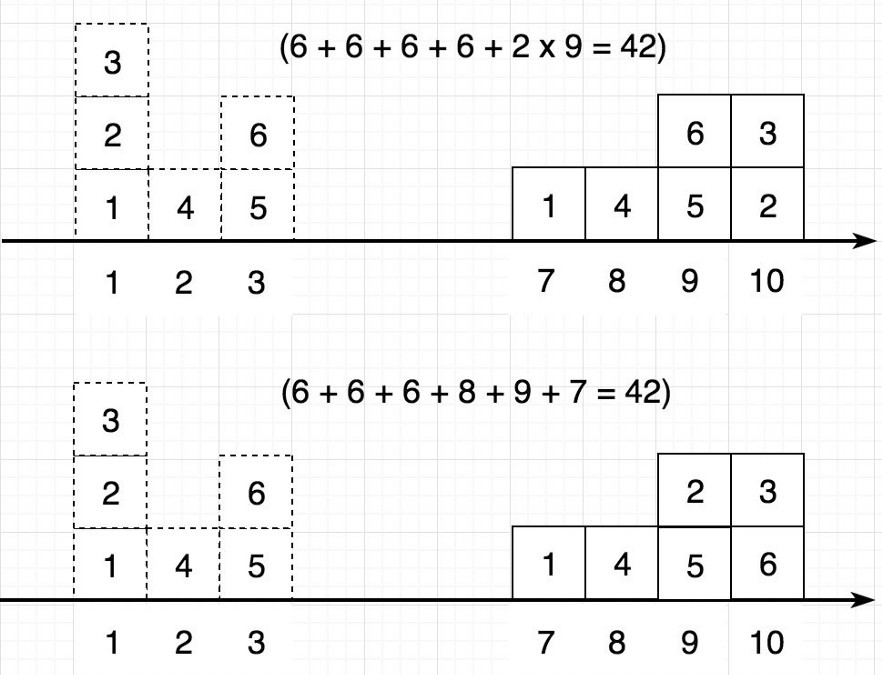2 ways of moving blocks from left to right.

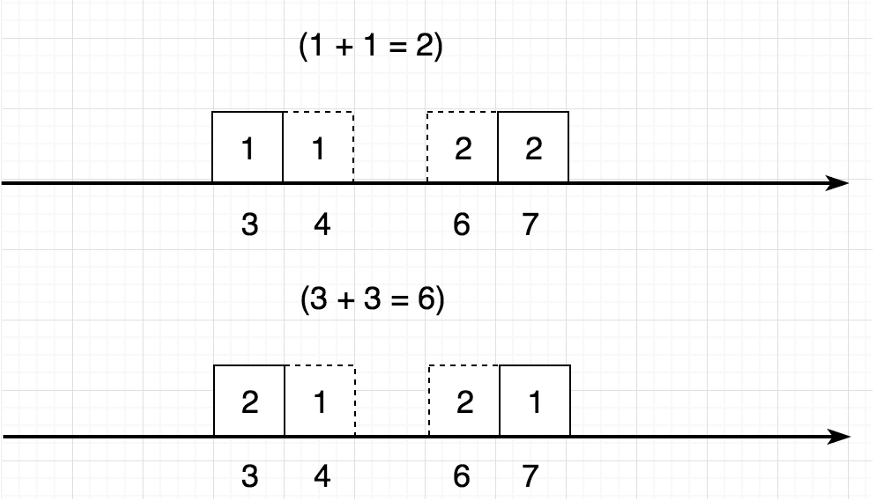
Above example gives the same energies ($42$) but there are usually different as below example,

Coding

from scipy.stats import wasserstein_distance

arr1 = [1,2,3,4,5,6]
arr2 = [1,2,3,4,5,6]
wasserstein_distance(arr1, arr2)

0.0
# they are exactly the same!

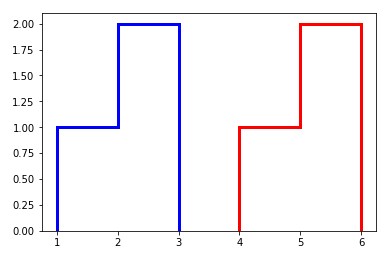
arr1 = [1,2,3]
arr2 = [4,5,6]
wasserstein_distance(arr1, arr2)
# 3.0000000000000004

import seaborn as sns
sns.distplot(arr1, kde=False, hist_kws={"histtype": "step", "linewidth": 3, "alpha": 1, "color": "b"})
sns.distplot(arr2, kde=False, hist_kws={"histtype": "step", "linewidth": 3, "alpha": 1, "color": "r"})

References

• What is an intuitive explanation of the Wasserstein distance?
• GAN — Wasserstein GAN & WGAN-GP
• An example of why we need to use EMD instead of Kolmogorov–Smirnov distance (video).

×Close