Kolmogorov–Smirnov Test^•

Last modified on 01 Oct 2021.

What & Why?

To check the similar distribution of 2 samples drawn from population. If these samples are normal, we can use T-test, but if they are not normal, we need to use KS-test. KS-test is a non-parametric test.

Null hypothesis ($H_0$): “Two samples drawn from population with the same distribution.”

👉 Read more about p-value. We use this value to evaluate the true/false of above null hypothesis.

The difference (in use) of T-test (need an assumption of nomality) and KS-test (don’t need),

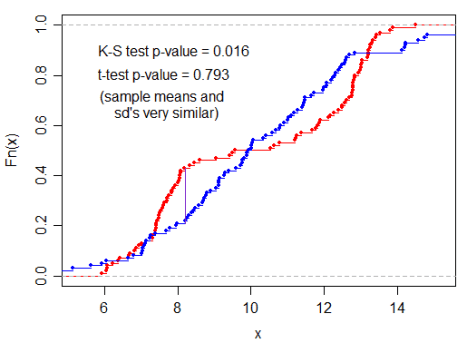
• Two samples have the same mean & standard deviation ⇒ p-value is high ⇒ cannot reject $H_0$ (not true)
• KS-test can detect the variance ⇒ p-value is low ⇒ we can reject $H_0$ ⇒ 2 samples are not the same distribution!!! (yep!)

How?

If the KS statistic is small or the p-value is high, then we cannot reject the hypothesis that the distributions of the two samples are the same.

Code?

from scipy import stats

# one-sample KS test
stats.kstest(x, 'norm')

# two-sample KS test
stats.ks_2samp(x, y)

References

• Matthew E. Clapham – 10: Kolmogorov-Smirnov test (video)
• An example of why we need to use EMD instead of Kolmogorov–Smirnov distance (video).

×Close