Last modified on 01 Oct 2021.
What’s the idea of SVM?
SVM (also called Maximum Margin Classifier) is an algorithm that takes the data as an input and outputs a line/hyperplane that separates those classes if possible.
Suppose that we need to separate two classes of a dataset. The task is to find a line to separate them. However, there are many lines which can do that (countless number of lines). How can we choose the best one?
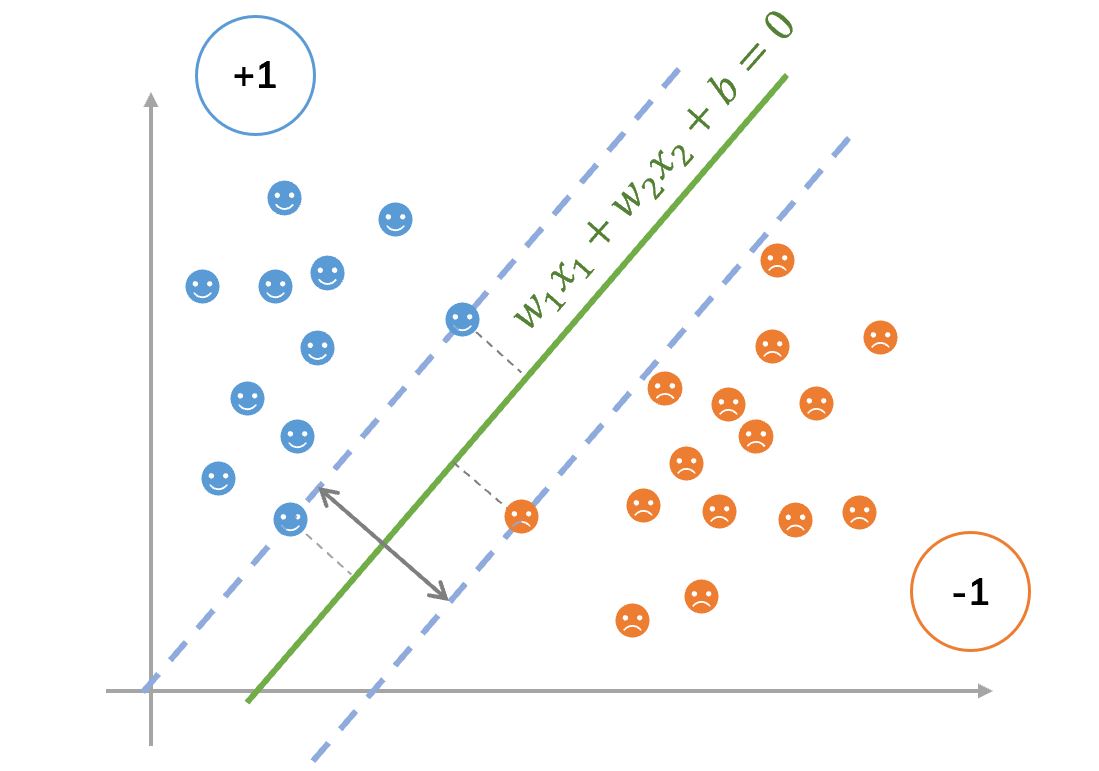
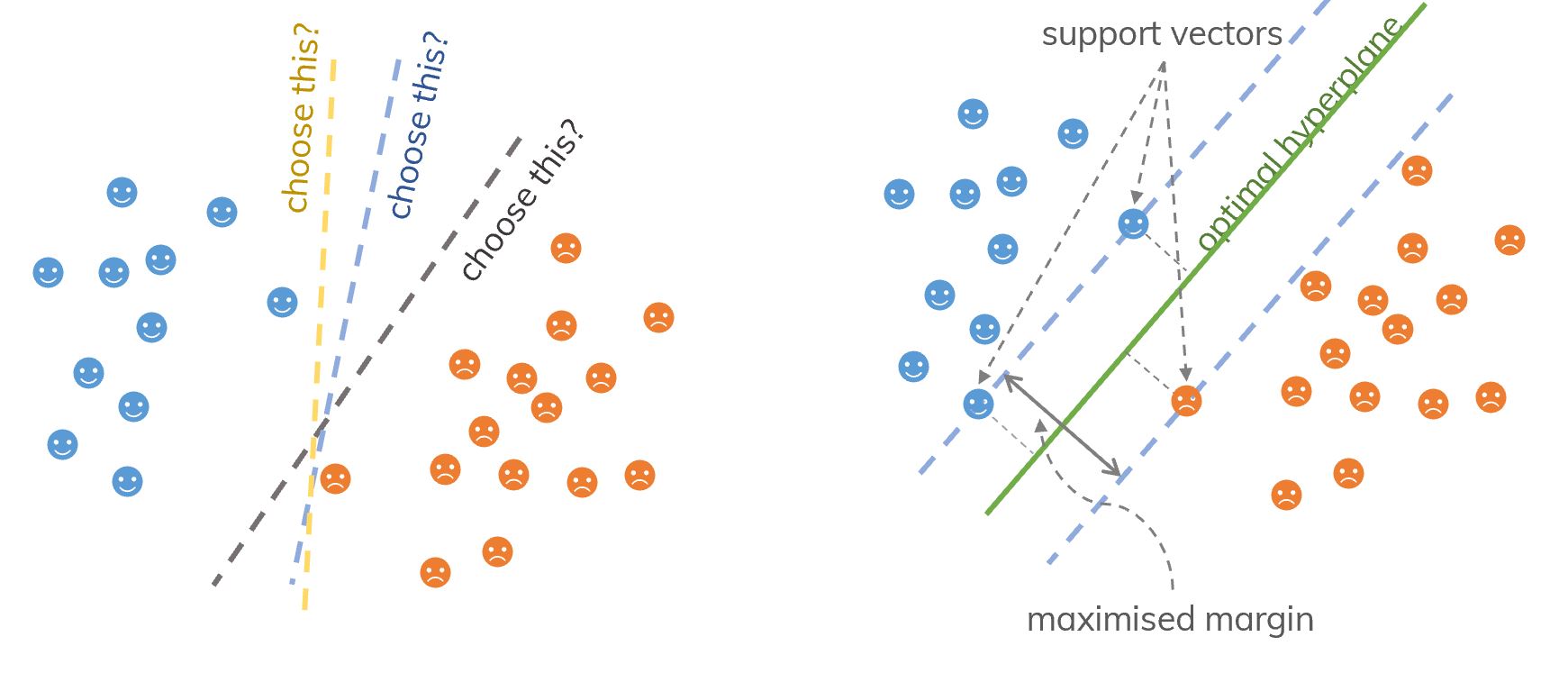 An idea of support vectors (samples on the margin) and SVM (find the optimal hyperplane).
An idea of support vectors (samples on the margin) and SVM (find the optimal hyperplane).
Using SVM with kernel trick
Most of the time, we cannot separate classes in the current dataset easily (not linearly separable data). We need to use kernel trick first (transform from the current dimension to a higher dimension) and then we use SVM. These classes are not linearly separable.
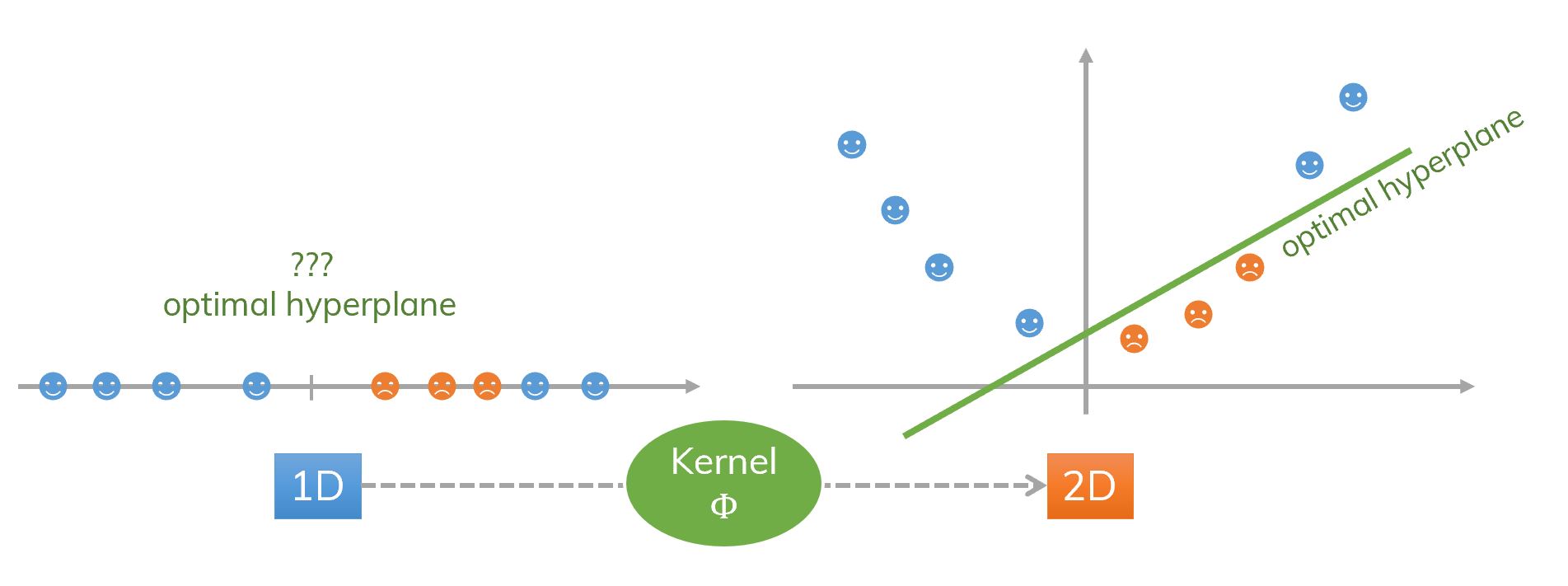 An idea of kernel and SVM. Transform from 1D to 2D. Data is not linearly separable in the input space but it is linearly separable in the feature space obtained by a kernel.
An idea of kernel and SVM. Transform from 1D to 2D. Data is not linearly separable in the input space but it is linearly separable in the feature space obtained by a kernel.
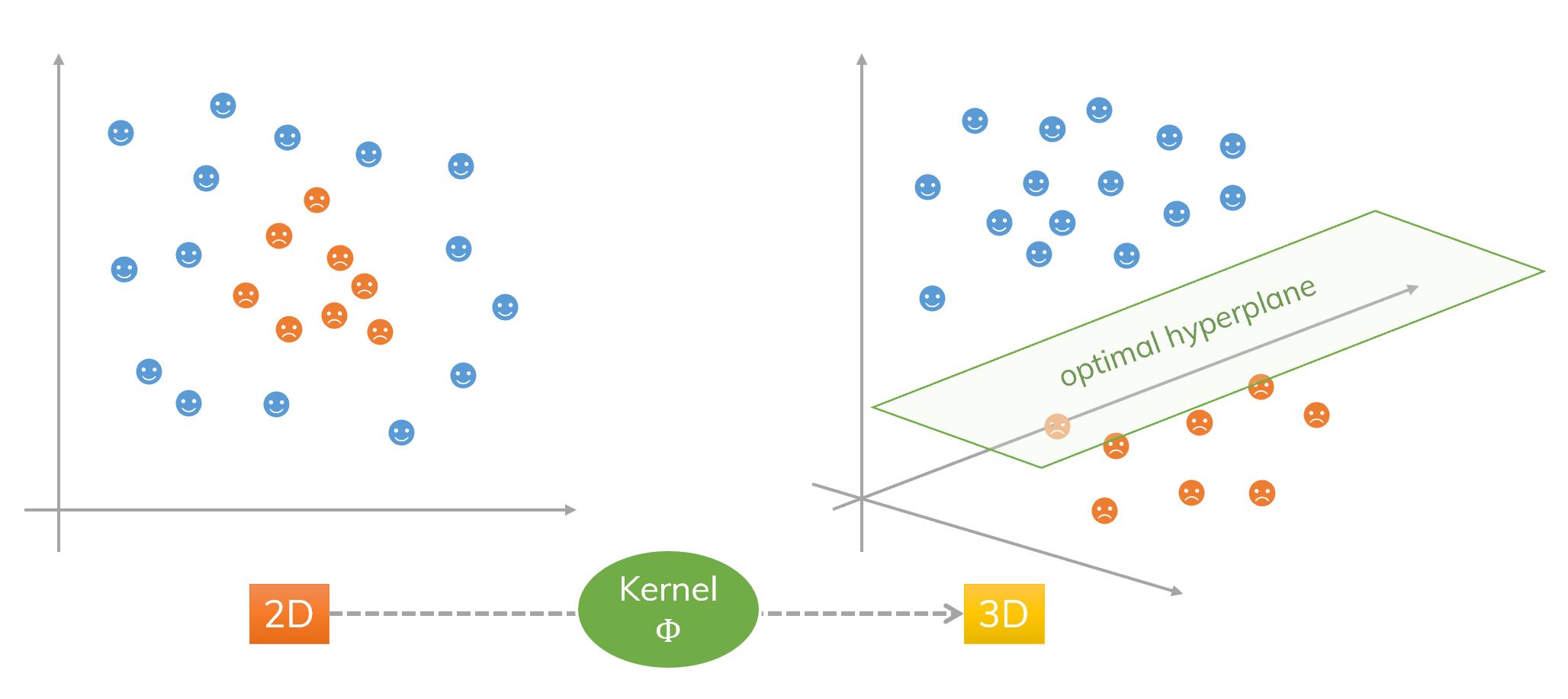 An idea of kernel and SVM. Transform from 2D to 3D. Data is not linearly separable in the input space but it is linearly separable in the feature space obtained by a kernel.
An idea of kernel and SVM. Transform from 2D to 3D. Data is not linearly separable in the input space but it is linearly separable in the feature space obtained by a kernel.
A kernel is a dot product in some feature space:
It also measures the similarity between two points and .
We have some popular kernels,
- Linear kernel: . We use
kernel = 'linear'insklearn.svm.SVM. Linear kernels are rarely used in practice. - Gaussian kernel (or Radial Basic Function – RBF): . It’s used the most. We use
kernel = 'rbf'(default) with keywordgammafor (must be greater than ) insklearn.svm.SVM. - Exponential kernel: .
- Polynomial kernel: . We use
kernel = 'poly'with keyworddegreefor andcoef0for insklearn.svm.SVM. It’s more popular than RBF in NLP. The most common degree is (quadratic), since larger degrees tend to overfit on NLP problems.[ref] - Hybrid kernel: .
- Sigmoidal: . We use
kernel = 'sigmoid'with keywordcoef0for insklearn.svm.SVM.
We can also define a custom kernel thanks to this help.
Choose whatever kernel performs best on cross-validation data. Andrew NG said in his ML course.
Good or Bad?
Advantages:
- Compared to both logistic regression and NN, a SVM sometimes gives a cleaner way of learning non-linear functions.
- SVM is better than NN with 1 layer (Perceptron Learning Algorithm) thanks to the largest margin between 2 classes.
- Accurate in high-dimensional spaces + memory effecient.
- Good accuracy and perform faster prediction compared to Naïve Bayes algorithm.[ref]
Disadvantages:
- Prone to overfitting: if number of features are larger than number of samples.
- Don’t provide probability estimation.
- Not efficient if your data is very big!
- It works poorly with overlapping classes
- Sensitive to the type of kernel used.
SVM used for?[ref]
- Classification, regression and outliers detection.
- Face detection.
- Text and hypertext categorization.
- Detecting spam.
- Classification of images.
- Bioinformatics.
Using SVM with Scikit-learn
from sklearn.svm import SVC
svc = SVC(kernel='linear') # default = 'rbf' (Gaussian kernel)
# other kernels: poly, sigmoid, precomputed or a callable
svc = svc.fit(X, y)
svc.predict(X)
# gives the support vectors
svc.support_vectors_
There are other parameters of sklearn.svm.SVM.
In the case of linear SVM, we can also use sklearn.svm.LinearSVC. It’s similar to sklearn.svm.SVG with kernel='linear' but implemented in terms of liblinear rather than libsvm, so it has more flexibility in the choice of penalties and loss functions and should scale better to large numbers of samples.[ref]
Meaning of some parameters
The Regularization parameter (C, default C=1.0): if C is larger, hyperplane has smaller margin but do a better job of classification and otherwise. This is how you can control the trade-off between decision boundary and misclassification term.
- Higher values of
Ca higher possibility of overfitting, the softmargin SVM is equivalent to the hard-margin SVM. - Lower values of
Ca higher possibility of underfitting. We admit misclassifications in the training data
We use this in the case of not linearly separable data; It’s also called soft-margin linear SVM.
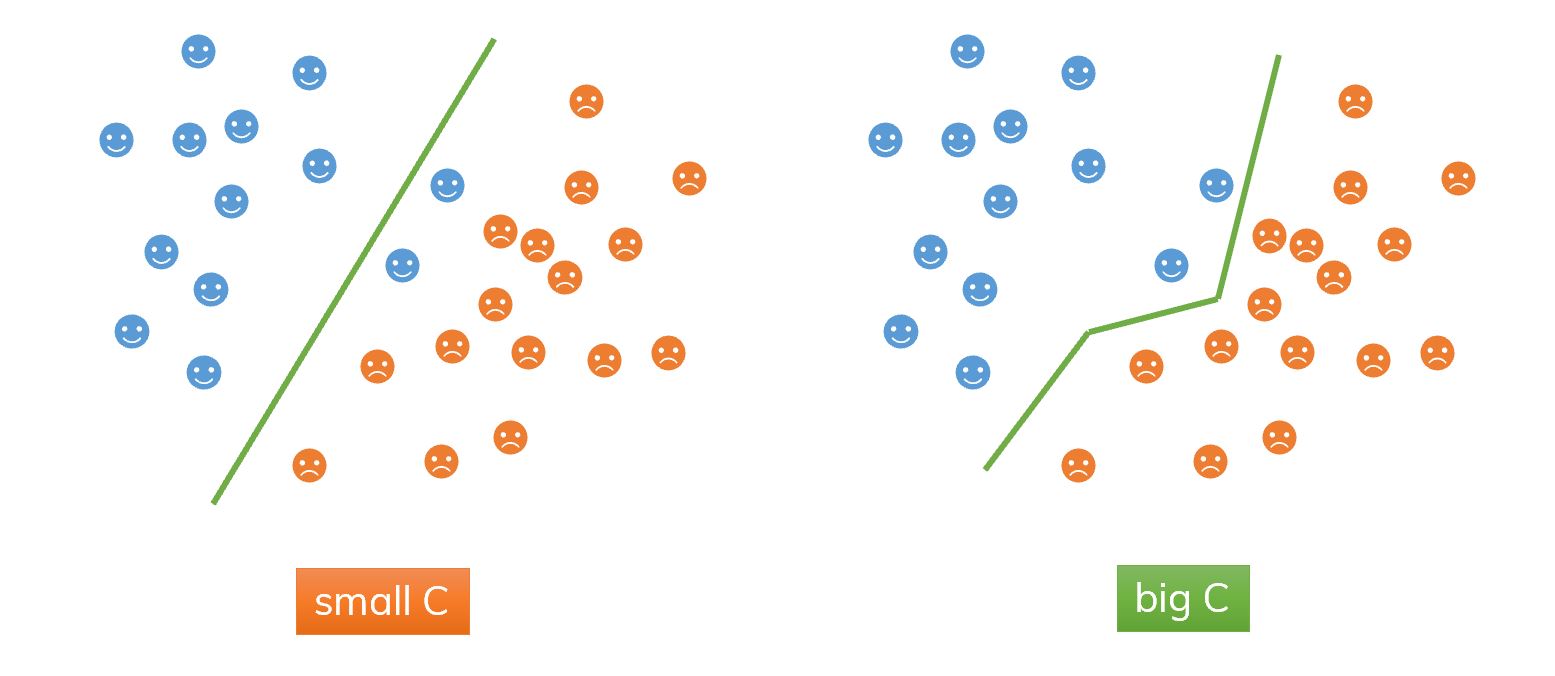 An illustration of using
An illustration of using C.
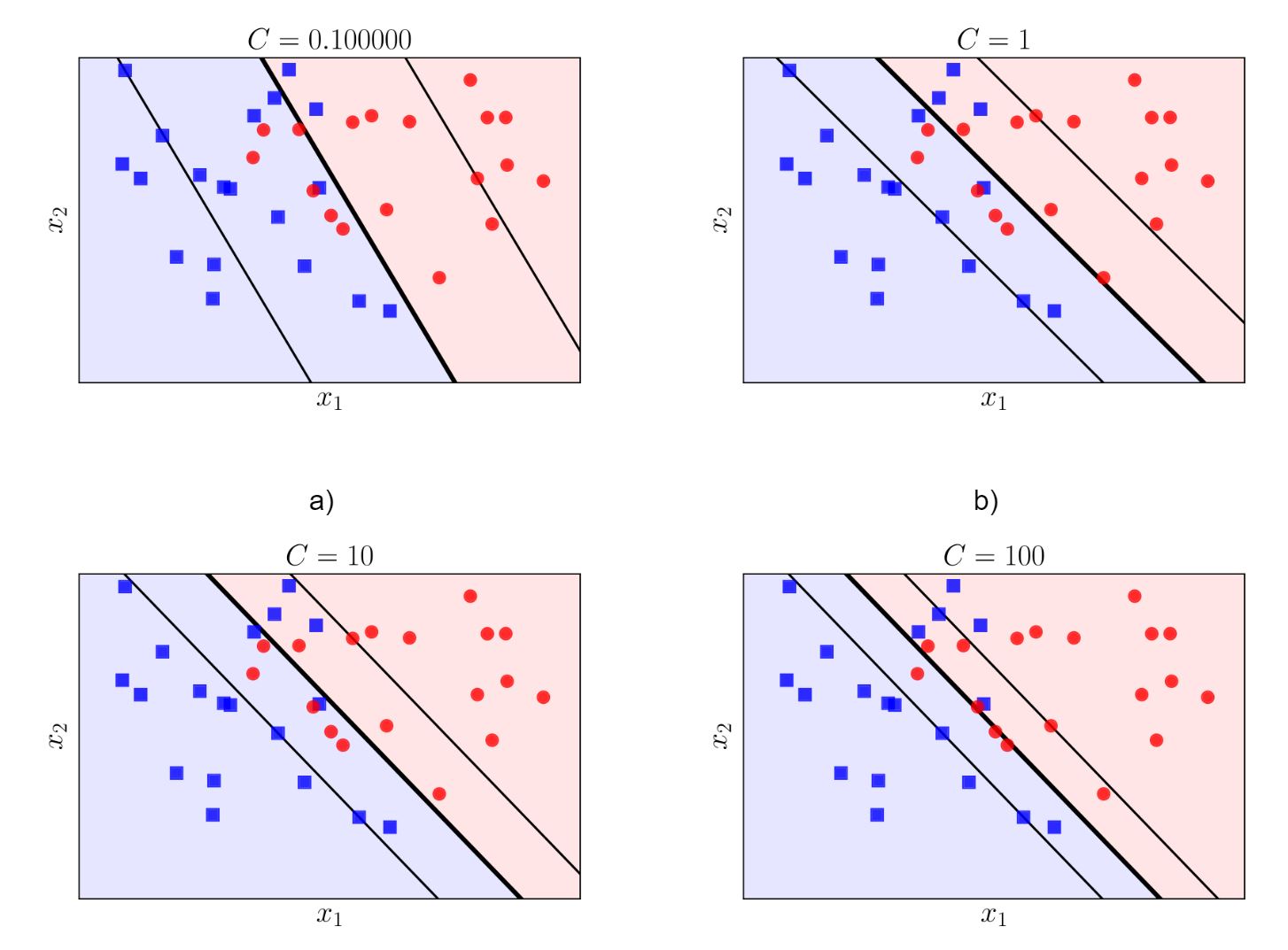 An illustration of using
An illustration of using C. Bigger C, smaller margin.[ref]
Gamma (gamma, default gamma='auto' which uses 1/n_features): determine the number of points to construct the hyperplane.
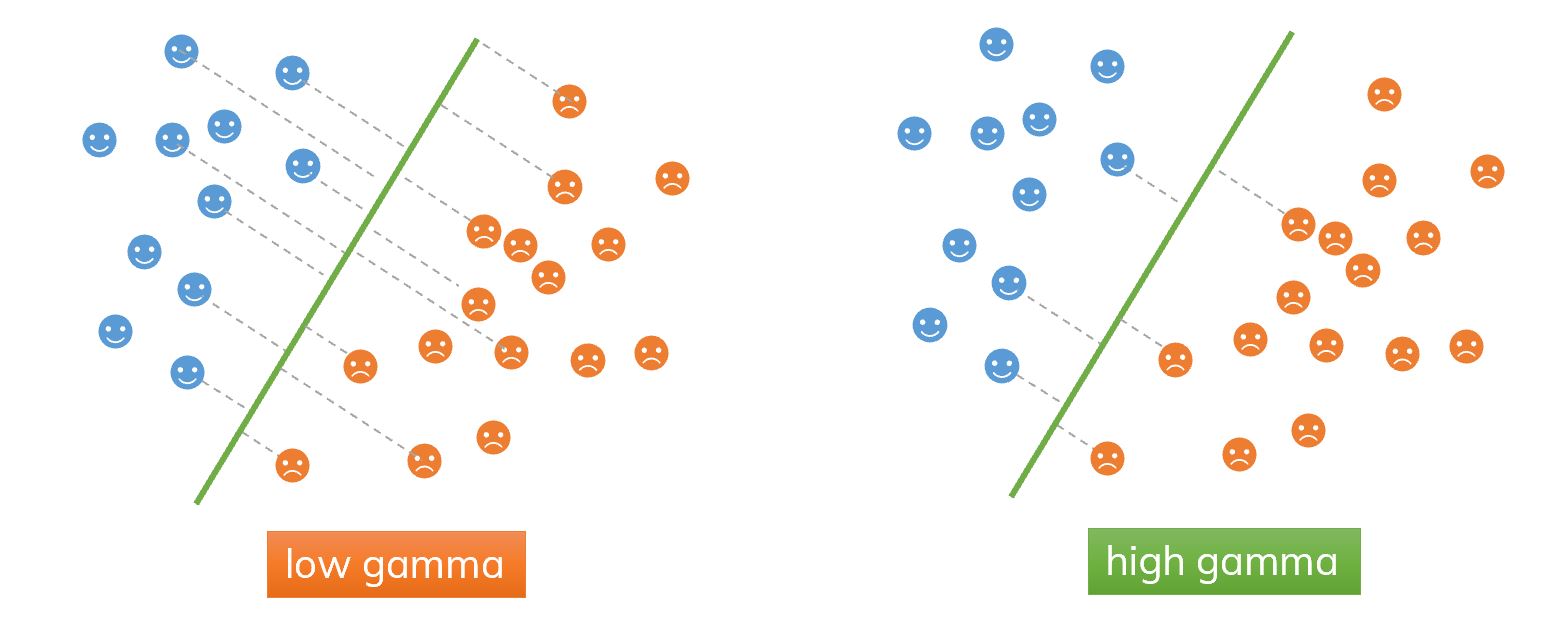 An illustration of using
An illustration of using gamma. In low-gamma case, we only consider points nearby the hyperplane, it may cause an overfitting.
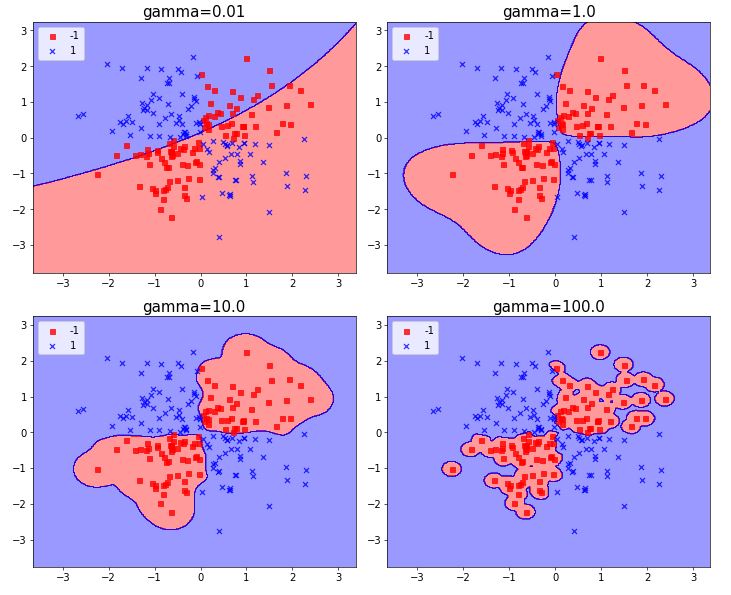 Bigger gamma, more change to get overfitting (in a XOR problem).
Bigger gamma, more change to get overfitting (in a XOR problem).
SVM in action
-
XOR problem to see the effect of
gammaandCin the case of using RBF kernel:–
-
Face Recognition[ref]:
–
References
- Scikit-learn – SVM official doc.
- Simplilearn – How Support Vector Machine Works | SVM In Machine Learning.
- Tiep Vu – Bài 19: Support Vector Machine.
- Jeremy Kun – Formulating the Support Vector Machine Optimization Problem.
- Tiep Vu – Bài 20: Soft Margin Support Vector Machine.
- Tiep Vu - Bài 21: Kernel Support Vector Machine.
- Alexander Statnikov, Douglas Hardin, Isabelle Guyon, Constantin F. Aliferis – A Gentle Introduction to Support Vector Machines in Biomedicine.
- Jake VanderPlas – In-Depth: Support Vector Machines. – Example: How to code and illustrate hyperplane and support vectors in Python?
- Chris Albon – Notes about Support Vector Machines.
- Andrew NG – My raw note when I learned the course Machine Learning on Coursera.

 We need to find an optimal hyperplane between 2 classes (find
We need to find an optimal hyperplane between 2 classes (find 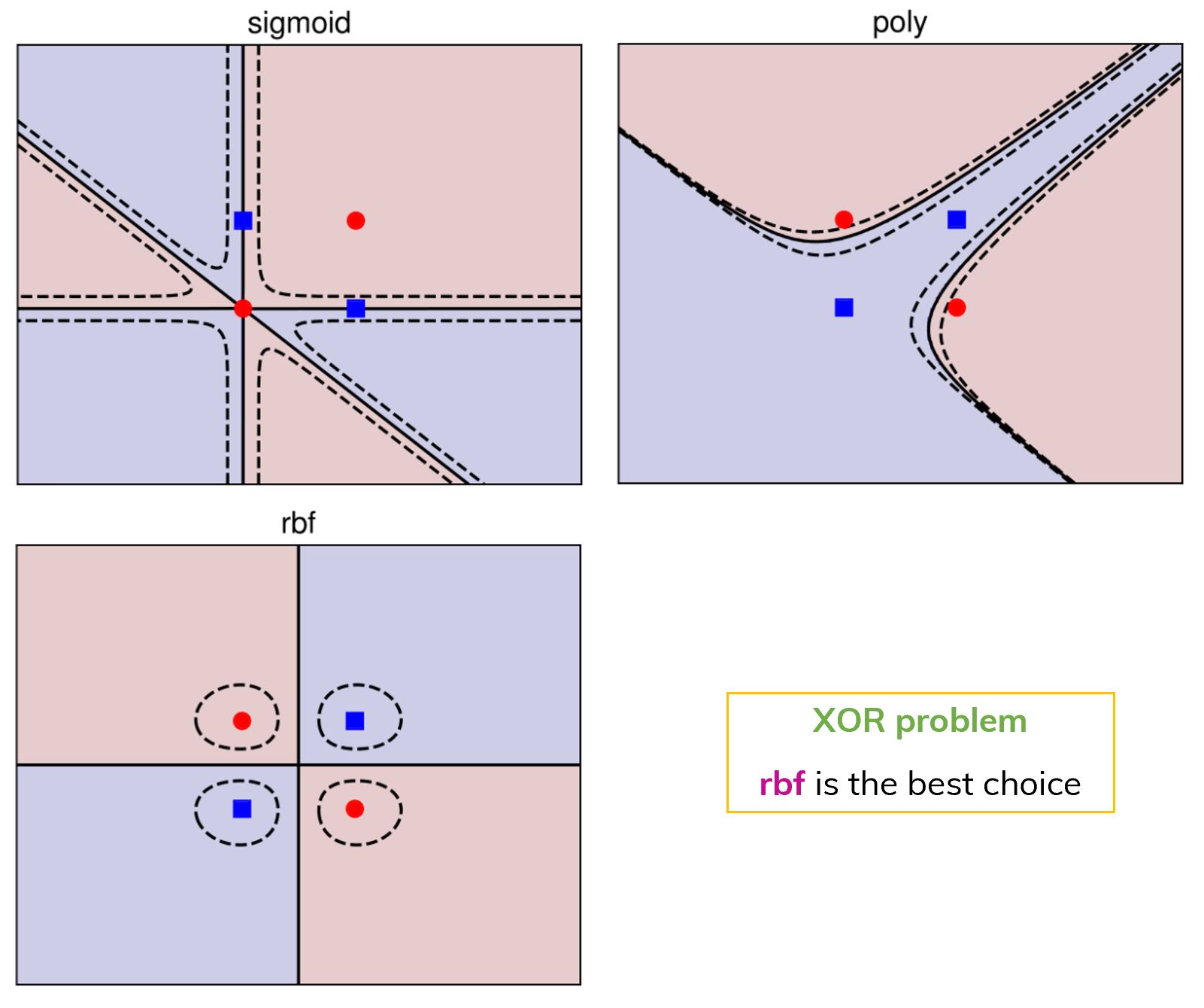 Using SVM with 3 different kernels in a
Using SVM with 3 different kernels in a 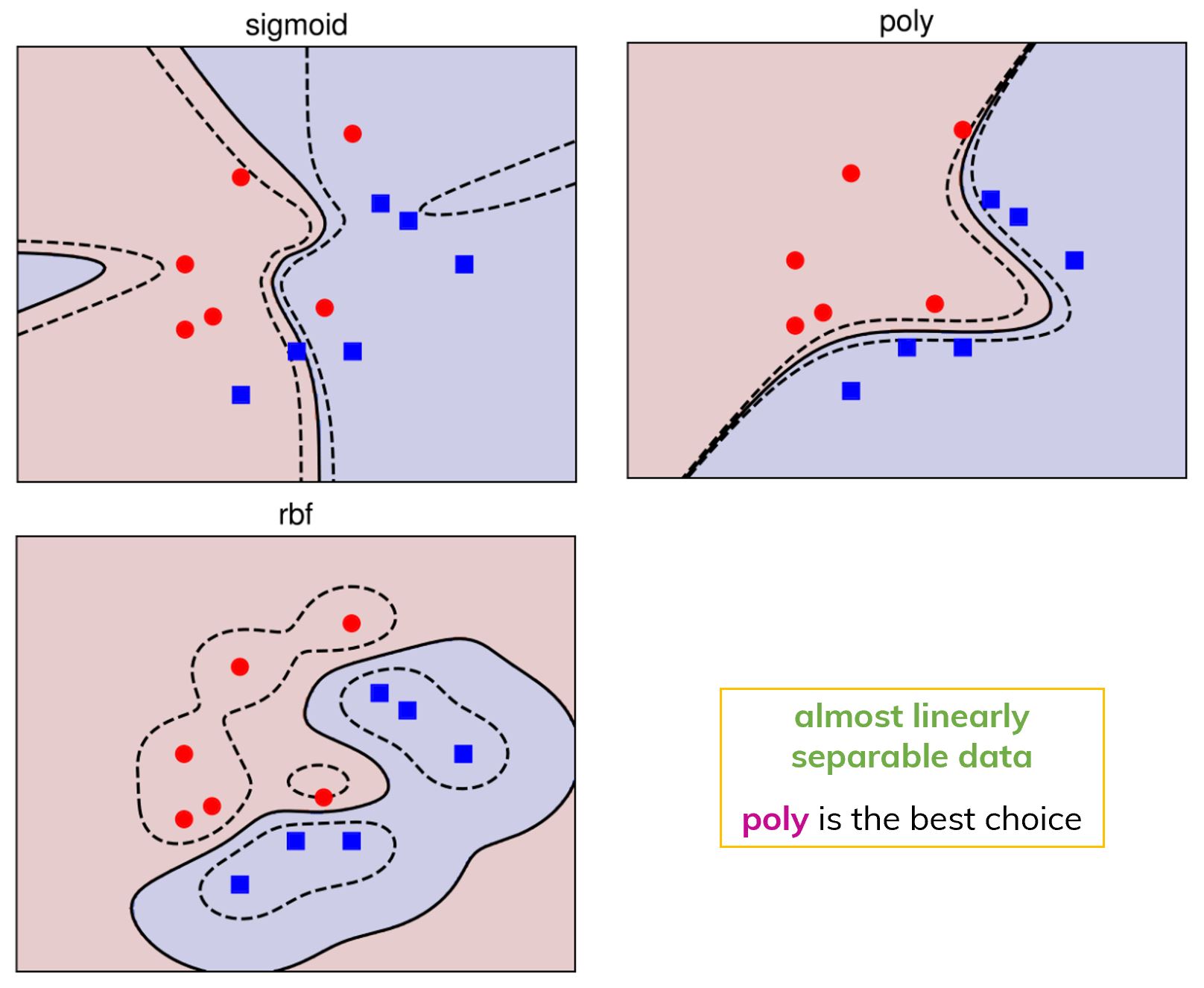 Using SVM with 3 different kernels in the case of almost linearly separable data. In this case, Polynomial kernel is the choice.
Using SVM with 3 different kernels in the case of almost linearly separable data. In this case, Polynomial kernel is the choice.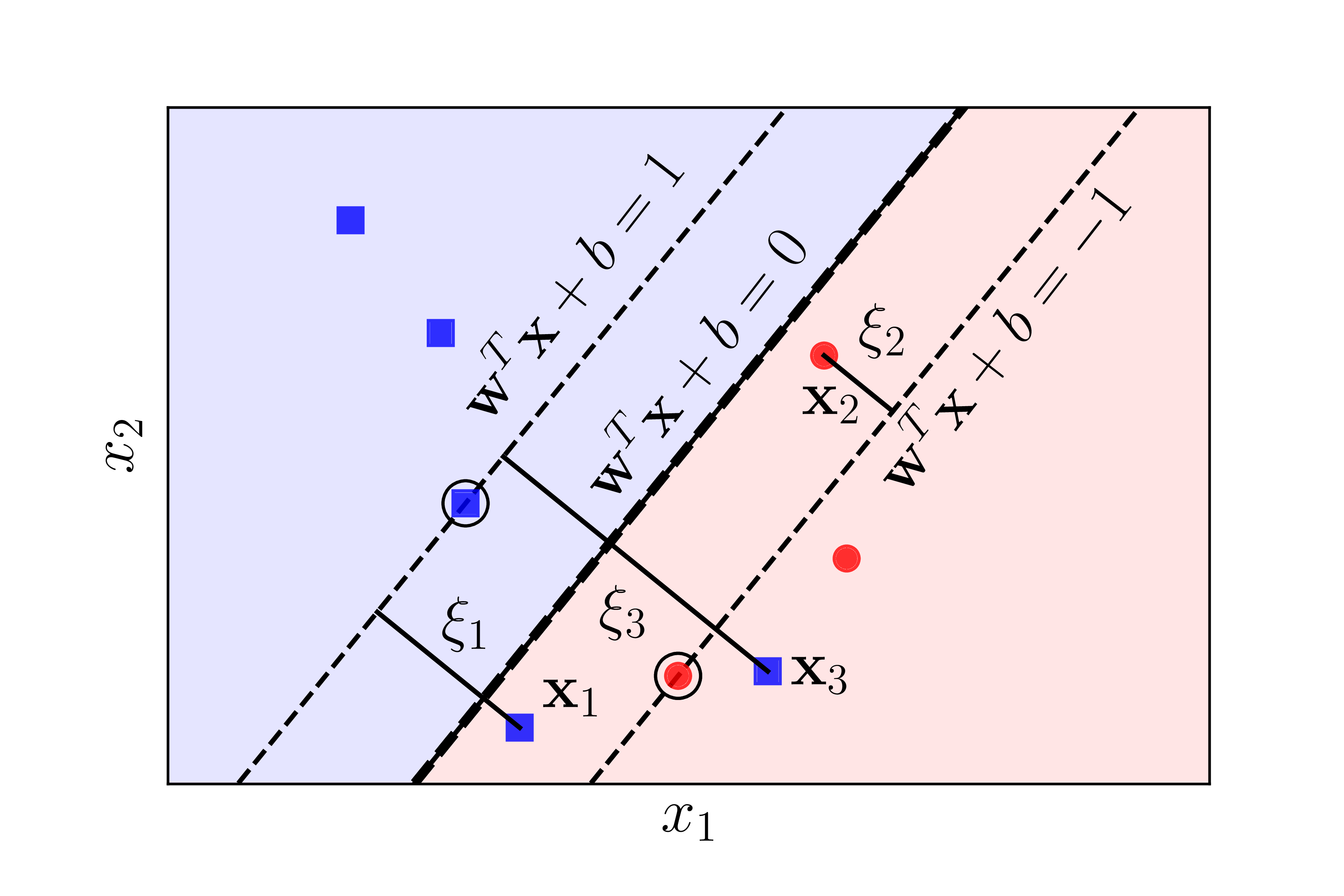 An introduction to slack variables.
An introduction to slack variables.